Implementing Newton Raphson Method in Python
Introduction
The Newton-Raphson method (also known as Newton’s method) is a Fast way to quickly find a good approximation for the root of a real-valued function f(x)=0.
This Method is iterative in nature hence is widely used in programming and computational algorithms
Its has a Quadratic Rate of convergence
It uses the idea that a continuous and differentiable function can be approximated by a straight line tangent to it.
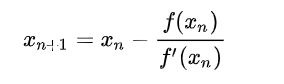
Limitations of Newton’s Method
Newton’s method may not work if there are points of inflection, local maxima or minima around x knot or the root.
if f`(X) = 0 then the tangent is parallel to x then there no root would occur
Implementation
Before Running the following program make sure you have installed the sympy library in Python 3 by typing following command in CMD
pip3 install sympyAs visible from formula we need to find f’(x) and the literate till we complete enough accuracy .
For differentiation the function we are using sympy library
we are checking for break conditions such as if our accuracy is enough or if the derivative is zero or not
""" Vineet Kumar Gupta """from sympy.parsing.sympy_parser import parse_expr
from sympy import *
x= symbols('x')""" Use these if you directly want to run """
#x0 = -20
#z= 10
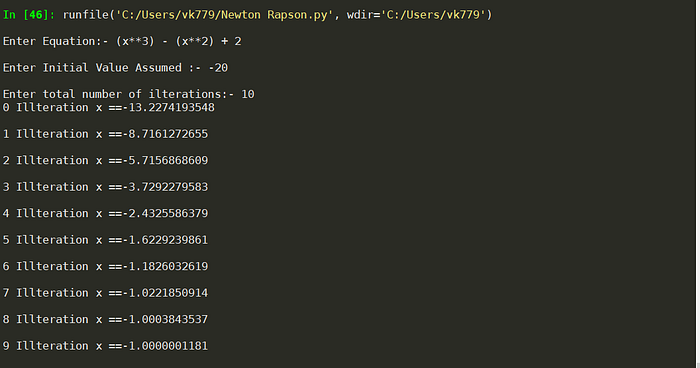
#eqn= "(x**3) - (x**2) + 2"eqn = input("Enter Equation:- ")
x0 = int(input("Enter Initial Value Assumed :- "))
z= int(input("Enter total number of ilterations:- "))expr = parse_expr(eqn)
expr_dash = expr.diff(x)def func(y):
return expr.subs(x,y)def derivFunc( y ):
return expr_dash.subs(x,y)def newtonRaphson(s, x ):
for m in range(s):
h = func(x) / derivFunc(x)
if(derivFunc(x) !=0 and abs(h) >= 0.0001):
x = x - h
print(m , "Illteration x ==%.10f"% x , sep=" ")
print("")
elif(abs(h) <= 0.0001):
print("Accuracy more than 4 places closing program")
break;
elif(derivFunc(x) ==0):
print("Derivative is 0 Closing Program")
break;newtonRaphson(z,x0)
Sample Output